¿Te va a tocar la Lotería de Navidad?
Esta calculadora predice si un número resultará premiado con el Gordo de la Lotería de Navidad en el próximo sorteo. La predicción tiene una exactitud de casi el 100%, o para ser más exactos un 99,999%. Sólo introduce cualquier número del 00000 al 99999 y pulsa el botón. Sabrás al instante la respuesta.
Tu predicción
El número introducido NO recibirá el primer premio en el próximo sorteo de #LoteríaNavidad. Esta predicción tiene una exactitud del 99.999% Clic para tuitearNo me lo creo ¿Cómo se calcula esto?
La predicción de si un número recibirá el primer premio en la próxima Lotería de Navidad la hago en base a una complicada fórmula matemática. Compartir las intríngulis de este método con todo el mundo sembraría el caos y la discordia. Pero como un poco de alboroto por estas fechas nunca viene mal, voy a contar mi secreto.
Es posible que la respuesta que recibiste del oráculo haya sido negativa. Es más, estoy seguro al 100% de que te ha dicho que el número que introdujiste no será premiado con el gordo. No te sorprendas, siempre dice lo mismo. Esta respuesta es acertada 99999 veces de cada 100000. Es decir, un 99,999% de las veces. Pocos métodos de predicción te van a asegurar un resultado tan preciso.
Entonces ¿Cuánto voy a ganar en la Lotería de Navidad?
Lo más que podemos hacer es calcular cuánto vale «de media» el décimo de lotería que has comprado por 20€. Por ejemplo, el reintegro por terminación te daría 20€, pero sólo hay un 10% de probabilidad de que toque. Multiplicando 20 por 0.1 (10%), sabemos que la posibilidad de ganar un reintegro le añade al décimo un valor de 2€. Si hacemos lo mismo con el resto de los posibles premios, nos sale lo siguiente.
| Premiados | Premio al décimo | Tipo de premio | Probabilidad | Valor |
| 1 | 400.000 € | El Gordo Primer Premio | 0,001% | 4,00 € |
| 1 | 125.000 € | Segundo Premio | 0,001% | 1,25 € |
| 1 | 50.000 € | Tercer Premio | 0,001% | 0,50 € |
| 2 | 20.000 € | Cuarto Premio | 0,002% | 0,40 € |
| 8 | 6.000 € | Quinto Premio | 0,008% | 0,48 € |
| 1794 | 100 € | La Pedrea | 1,794% | 1,79 € |
| 2 | 2.000 € | Aproximación primer premio | 0,002% | 0,04 € |
| 2 | 1.250 € | Aproximación segundo premio | 0,002% | 0,03 € |
| 2 | 960 € | Aproximación tercer premio | 0,002% | 0,02 € |
| 97 | 100 € | Centena primer premio | 0,097% | 0,10 € |
| 97 | 100 € | Centena segundo premio | 0,097% | 0,10 € |
| 97 | 100 € | Centena tercer premio | 0,097% | 0,10 € |
| 198 | 100 € | Centena cuartos premios | 0,198% | 0,20 € |
| 999 | 100 € | Dos últimas cifras primero | 0,999% | 1,00 € |
| 999 | 100 € | Dos últimas cifras segundo | 0,999% | 1,00 € |
| 999 | 100 € | Dos últimas cifras tercero | 0,999% | 1,00 € |
| 9999 | 20 € | Reintegro a la última cifra | 9,999% | 2,00 € |
Sumando todos los valores, resulta que un décimo vale en realidad 14€. Es decir, que por cada décimo que compres, vas a perder 6€ de media. Cuanto más juegues, más pierdes.
Eso sin tener en cuenta que la probabilidad de obtener uno de los premios más grandes es prácticamente cero. Esto significa que, por ejemplo, para que realmente el primer premio aporte sus 4€ al valor que hemos calculado, tendrías que jugar muchísimas veces hasta que toque. Y eso, como te ha dicho el oráculo, es prácticamente imposible.
El símil del arroz
Imagina que tienes un saco con tres kilos de arroz. Es un buen saco. Según algunos cálculos, en todo ese montón hay aproximadamente 100.000 granos de arroz. Como hay algunos más, le quitamos un puñado, si quieres. Uno de los granos está pintado de negro y mezclado con los demás. Con los ojos tapados y usando una pinza, atrapas un grano al azar ¿Crees que atraparás el grano negro?
Puedes repetir este experimento tantas veces como quieras. Probablemente te aburrirás antes de encontrar el grano negro, pero este juego tiene dos ventajas con respecto a la Lotería:
- No tienes que esperar al próximo sorteo, si te divierte puedes hacerlo sin parar durante días. Hay mucho arroz.
- No te cuesta dinero cada vez que fallas. Salvo lo que te haya costado el arroz. Pero si tienes cuidado seguirá siendo apto para el consumo.
Vale, pero ¿Y la pedrea, reintegros y demás?
Es habitual pensar que se puede recuperar el dinero gracias a los premios menores, que sí tienen una probabilidad aceptable de tocar. Se suele poner esperanza en la pedrea. Son 1794 números que reciben 100€. Si te toca uno de esos amortizas al menos 5 décimos ¿No?
Pues bien, es muy poco probable que toque una pedrea. La probabilidad es de aproximadamente el 1.8%. Pero es cierto que las aproximaciones y terminaciones, otros 3486 números, dan el mismo premio. Sumando todas esas opciones, la probabilidad de ganar 100€ aumentan hasta un 5.3%. No es muy alta, pero tal vez jugando varios números se puedan mejorar las opciones.
| Probabilidad de ganar algo (incluido reintegro) | 15,3% |
| Probabilidad de premio grande (más de 100€) | 0,019% |
| Probabilidad de ganar 100€ | 5,3% |
Estos porcentajes son aproximados, ya que hay números que se llevan a la vez un premio y un reintegro. Por tanto, las probabilidades no se sumarían. Pero al ser tan baja la probabilidad de obtener un premio diferente de un reintegro, el resultado real se acercaría bastante.
Probabilidad de perder dinero
Con estos datos en la mano, me hice la siguiente pregunta: ¿Qué probabilidad hay de que acabe perdiendo dinero en función de la cantidad de décimos que juegue? Los supuestos son los siguientes.
- Compras 1 décimo, así que debes recuperar 20€. Lo conseguirás si te toca algo, lo que sea (15.3% de probabilidad). Por tanto perderás algo de dinero el resto de las veces (84.7%).
- Si tienes 2 décimos, debes recuperar 40€. A no ser que tengan la misma terminación, ganar dos reintegros es imposible. Sólo nos quedan los premios grandes. La probabilidad de que ninguno de los dos obtenga un premio de 100€ o más es 89.7% ¡Hemos empeorado!
A partir de ahí, hasta los 5 décimos, las opciones mejoran ligeramente. Sin embargo, con 6 décimos la progresión se frena. Ya no nos vale con que toque un premio de 100€. Dado que hemos invertido 120€, necesitamos al menos un premio de 100€ y un reintegro. O dos premios de 100€. Para los 7 décimos, la probabilidad vuelve a empeorar y la historia se repite hasta los 10 números. De hecho, es más fácil perder dinero con siete números que con uno.
Basta de matemáticas ¡A programar!
Hasta aquí he estado haciendo algunas simplificaciones. En general, la realidad es ligeramente peor de lo que he calculado, ya que hay premios que no son compatibles. Ten en cuenta que, por ejemplo, si te toca una pedrea no te puede tocar a la vez un quinto premio. Por tanto la probabilidad de ganar una de las dos cosas es ligeramente inferior.
Para no liarme más con esto, hice un programa que simula un sorteo en el que juegas N números. Este experimento se repite un millón de veces y se obtiene una estadística de cuántas veces has salido perdiendo. Este es el resultado para los 15 primeros valores de N.
| Números jugados | Probabilidad de perder dinero |
| 1 | 86,25% |
| 2 | 89,13% |
| 3 | 85,17% |
| 4 | 80,78% |
| 5 | 76,61% |
| 6 | 83,25% |
| 7 | 89,81% |
| 8 | 91,86% |
| 9 | 91,39% |
| 10 | 89,96% |
| 11 | 90,45% |
| 12 | 92,59% |
| 13 | 94,37% |
| 14 | 95,09% |
| 15 | 94,96% |
Simulación «ludópata» que juega hasta 100 números
Es decir, que por lo general, la probabilidad de acabar perdiendo dinero es mayor cuantos más números lleves. Esta probabilidad sigue aumentando hasta estabilizarse alrededor del 98.5%. Es decir, que cuando apuestas fuerte, es prácticamente seguro que perderás.
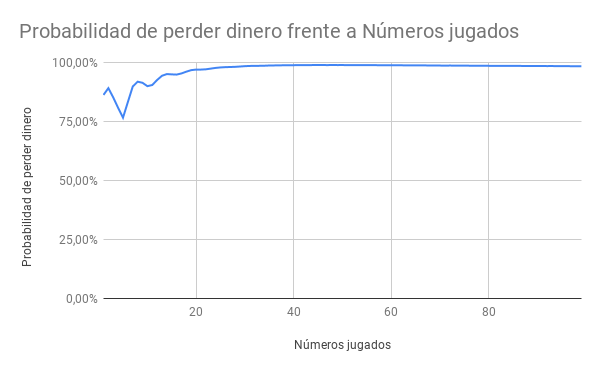
Por mencionar algún dato curioso: lo óptimo sería jugar cinco números, ni uno más. Aunque tampoco este caso es recomendable, ya que perderás tres de cada cuatro veces, habiendo gastado 100€. Ya vimos antes que cuanto más juegas más pierdes. Acabamos de demostrar que, además, cuanto más juegues más probable es que pierdas.
En #LoteríaNavidad, lo óptimo es jugar cinco números. Pero, aún así, pierdes tres de cada cuatro veces. Clic para tuitear¿Y si cae aquí?
En muchas ocasiones jugamos a la lotería por miedo. Aunque racionalmente sabes que es una mala inversión, sigues comprando «por si acaso». No vaya a ser que les toque a los demás y no a ti. Los profesionales de la publicidad conocen este miedo y lo explotan en sus campañas para mejorar las ventas. Seguro que se te ocurren muchos ejemplos.
La visibilidad del resultado improbable
Además, por mucho que nuestro cerebro nos diga que es prácticamente imposible que nos toque el Premio Gordo, seguimos pensando que se podría dar el caso. La evidencia a nuestro alcance nos empuja a pensar así. Por ejemplo, en las noticias del día 22 de diciembre verás gente celebrando un premio. Sin embargo, esas personas no son una muestra representativa del resultado. Piensa que nadie sale en el Telediario gritando «¡No me ha tocado nada! ¡He tirado el dinero!». Pero esa es, en realidad, la situación de la práctica totalidad de los que han jugado.
El millonario conocido
También solemos recordar a gente que conocemos que resultó premiada en alguna ocasión y tendemos a pensar que esa persona podríamos ser nosotros esta vez. Estos casos tampoco son representativos, y tampoco es tan extraño que conozcamos a algún afortunado. Veamos.
- Según he leído en algún sitio, llegamos a conocer a unas 2000 personas en nuestra vida.
- Un español juega de media algo más de 60€ (datos de 2017). Esto son 3 décimos, pero supongamos que sólo juegan uno.
- Por tanto, la probabilidad de que alguno de tus conocidos reciba un premio especial (de más de 100€) es de un 31,6%. Eso sólo contando el sorteo de este año.
- Pese a todo, la probabilidad de que seas tú el que recibe uno de estos premios sigue siendo de 0.019%. Prácticamente cero.
Por tanto, no es extraño que conozcas o sepas de alguien que ha ganado dinero en la lotería. Recuerda el saco de arroz del que hablaba antes. Si sumerges un vaso grande y lo sacas lleno arroz, no es tan difícil que en ese vaso hayas atrapado el grano pintado de negro.
El miedo a arrepentirse
Hay estudios psicológicos que demuestran que tomamos decisiones irracionales por miedo al arrepentimiento, no sólo en lo que se refiere a la lotería, sino en la vida en general. En el muy improbable caso de que un número que has rechazado resulte premiado, los expertos avisan de que el remordimiento no es tan doloroso como uno suele anticipar. Sobre todo hay que hacer un ejercicio de reflexión antes de tomar la decisión de jugar o no jugar. Debes ser consciente de los motivos por los que tomas tu decisión, saber que no lo hiciste sólo por lo que viste en un anuncio o por lo que escribió alguien en un blog. Tus motivos deben ser sólidos y apoyarse en datos y evidencias reales.
Me has robado la ilusión ¡Te odio!
Bueno, bueno, no nos pongamos tiernos todavía. En primer lugar, recuerda que yo no tengo nada que ver con la organización del sorteo de Lotería de Navidad. Ni siquiera creo que me vayan a dar RT, fav, ni nada de eso. Lo único que he hecho es analizar unos datos que son accesibles para todos y compartir contigo mis conclusiones. Si aun así, sigues queriendo decirme cuánto me aprecias, deja un comentario en esta página y debatimos.
Se pueden encontrar motivos para jugar: la tradición, la emoción, hacer un regalo… Pero siempre con conocimiento y sabiendo realmente en qué consiste este juego. Nunca deberías poner tus esperanzas de futuro en un juego de apuestas. Y recuerda, cuando estés comprobando y rompiendo tus décimos, en lugar de «¡Qué mala suerte tengo!», exclama mejor «¡Qué congruencia probabilística!».
Otro año que no me ha tocado la #LoteríaNavidad ¡Maldita congruencia probabilística! Clic para tuitear¡Gracias por leer!
